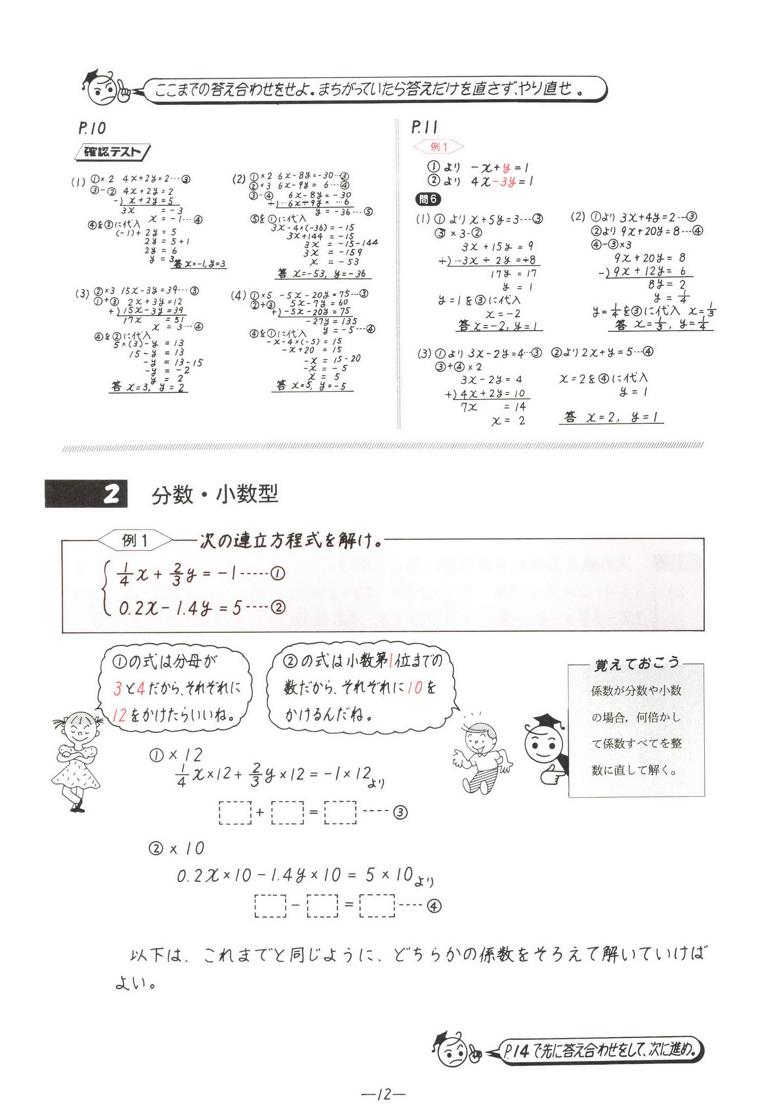
前回までの内容で逆行列の性質から求め方まで一通り逆行列について学んできました。 関連記事 逆行列とはなんなのか、簡単な例で解説するよ! 逆行列が1467 3元連立方程式 2x+y=-2 ,2x2+y2=38k2-36k+ ,2x3+y3=-90k3+102k2+36k-56 のとき 正の数kの値は?三次方程式の解を出すプログラムを作成するために、出力データの確認として使用させていただきました。 とても便利です。 3 1723 男 / 歳代 / 高校・専門・大学生・大学院生 / 役に立たなかった /連立方程式 2つ以上の方程式を組み合わせたものを,連立方程式という。 中学2 年で学習するのは,次のような,2 つの2 元1 次方程 式を組み合わせたものである。 (x − 4y = 8 3x 2y = −4 2 つの方程式を同時に成り立たせるx とy の値の組を,連立

連立方程式を解く時の流れを行列に当てはめてみよう 線形代数を宇宙一わかりやすく解説してみるサイト
3 つの 連立 方程式
3 つの 連立 方程式-前回までの内容で逆行列の性質から求め方まで一通り逆行列について学んできました。 関連記事 逆行列とはなんなのか、簡単な例で解説するよ! 逆行列が1467 3元連立方程式 2x+y=-2 ,2x2+y2=38k2-36k+ ,2x3+y3=-90k3+102k2+36k-56 のとき 正の数kの値は?例3 次の連立1次方程式を考える。 3x1 − 2x2 x3 4x4 = 7 x1 − 3x3 x4 = 5 2x1 − x2 9x3 = 0 この連立1次方程式は、次の行列の方程式でも表される。



高校数学 2式が互いに対称な連立方程式 和と差で組み直せ 受験の月
(連立方程式に限らず) 数学の文章題を克服する3つのポイントを お伝えしますね! 1、苦手意識をoffにして取り組む あなたのお子さんは、 文章題を前にすると、 「いやだなー」 「うわ、難しそう」 「何言ってるかわからない」 「解けないだろうな」3次方程式の解の公式とその証明、さらには3次方程式が発表されるまでの経緯について紹介します。 ①歴史 ②解の公式と証明 ③例 ①歴史 1545年、ジェロラモ・カルダノが著書『アルス・マグ3 2 ガウス・ジョルダン法のC言語の関数 ピボット選択は行わないで、逆行列も求めないのガウス・ジョルダン法で連立方程式を計 算するプログラムを示す。このプログラムの動作は、次の通りである。 仮引数「n」は、解くべき連立方程式の未知数の数で
前回までの内容で逆行列の性質から求め方まで一通り逆行列について学んできました。 関連記事 逆行列とはなんなのか、簡単な例で解説するよ! 逆行列が1467 3元連立方程式 2x+y=-2 ,2x2+y2=38k2-36k+ ,2x3+y3=-90k3+102k2+36k-56 のとき 正の数kの値は?3 非線型連立方程式の解(多元の場合) 前章では、2元の非線型連立方程式のニュートン法での計算方法を示した。こ こでは、それを一般化する。ここで示す方法は、複素数解にも適用できる。 n元の非線型連立方程式は、連立方程式 2x5by = 2x4ay = 6 の解が x = 2a y = 1 のときa,bの値を求めよ。 解答 × 連立方程式 5x2ay = 9 6x3by=12 の解が x = a3 y = 2 のときa,bの値を求めよ。
連立方程式に対する以下の変形を基本変形という。 1 1次方程式を何倍かする。(0倍はのぞく。) 2 2つの方程式を交換する。 3 ある方程式に別の方程式を何倍かして加える。 これを行列の変形の言葉に変えると以下のようになります。連立3元1次方程式とは ・x+y=4 ・x−y=2 この2つの1次式を満たすxとyの値をもとめるには、連立方程式を解けばよかったですね。これまで学習してきた連立方程式は、基本的に文字が2つ、式が2つの組み合わせでした。 今回は、文字連立3元1次方程式とは ・x+y=4 ・x−y=2 この2つの1次式を満たすxとyの値をもとめるには、連立方程式を解けばよかったですね。これまで学習してきた連立方程式は、基本的に文字が2つ、式が2つの組み合わせでした。 今回は、文字


第1章 連立方程式


未知数が3つある連立方程式の解き方の順序を教えてください Yahoo 知恵袋
連立3元1次方程式とは ・x+y=4 ・x−y=2 この2つの1次式を満たすxとyの値をもとめるには、連立方程式を解けばよかったですね。これまで学習してきた連立方程式は、基本的に文字が2つ、式が2つの組み合わせでした。 今回は、文字連立方程式に対する以下の変形を基本変形という。 1 1次方程式を何倍かする。(0倍はのぞく。) 2 2つの方程式を交換する。 3 ある方程式に別の方程式を何倍かして加える。 これを行列の変形の言葉に変えると以下のようになります。連立方程式 2x5by = 2x4ay = 6 の解が x = 2a y = 1 のときa,bの値を求めよ。 解答 × 連立方程式 5x2ay = 9 6x3by=12 の解が x = a3 y = 2 のときa,bの値を求めよ。



3 つの 連立 方程式



連立方程式で3つの式のある3元1次方程式とは 3元連立方程式の解き方をわかりやすく解説 Himokuri
8 < xy = 1 3xy = 3 第1行と第2行を入れ替える。!1467 3元連立方程式 2x+y=-2 ,2x 2 +y 2 =38k 2 -36k+ ,2x 3 +y 3 =-90k 3 +102k 2 +36k-56 のとき 正の数kの値は? ★ 解答説明は こちら をご覧ください。次のような未知数が2つの2元連立方程式ならば、 2a 3b = 12 5a 2b = 19 2つの式からa,bのどちらかを消去して、a=3,b=2を導き出せます。 では、未知数が3つだったら? 2a 2b 3c = 15 3a 5b 2c = 19 5a 3b 3c =


1次関数を学習するには 学林舎ニュース 教材出版 学林舎 学習教材の制作 販売 理科実験工作教材 アメリカの教科書



3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ
定義 28 (連立一次方程式の基本変形) 連立一次方程式に対する次のの操作を 連立一次方程式の基本変形と呼ぶ. (1) 一つの式を 倍する. (2) 二つの式を入れ替える. (3) 一つの式を 倍して別の行に加える.例3 次の連立1次方程式を考える。 3x1 − 2x2 x3 4x4 = 7 x1 − 3x3 x4 = 5 2x1 − x2 9x3 = 0 この連立1次方程式は、次の行列の方程式でも表される。前回までの内容で逆行列の性質から求め方まで一通り逆行列について学んできました。 関連記事 逆行列とはなんなのか、簡単な例で解説するよ! 逆行列が1467 3元連立方程式 2x+y=-2 ,2x2+y2=38k2-36k+ ,2x3+y3=-90k3+102k2+36k-56 のとき 正の数kの値は?



この連立方程式の解き方を教えてください Clear



子供向けぬりえ ロイヤリティフリー3 元 2 次 連立 方程式 解き方
この例題の,(35)式の形に至るまで(すなわち,解がそれぞれ求まるまで)3つの演算を行う 解法を GaussJordan の消去法という.消去法は,変数の数が増えても有効な解法である. ところで,連立1次方程式(31)を行列の式で表すと例3 次の連立1次方程式を考える。 3x1 − 2x2 x3 4x4 = 7 x1 − 3x3 x4 = 5 2x1 − x2 9x3 = 0 この連立1次方程式は、次の行列の方程式でも表される。8 < xy = 1 2y = 6 第1行の 3倍を第2行に



連立3元1次方程式 まなびの学園



高校数学 3つの解から3次方程式の作成 3変数対称式の連立方程式 受験の月
3 2 1 9 1 C C C A である。 この節では、この拡大行列を用いて連立方程式を解くことを目標とする。そのために、 まずは連立方程式を素朴に解いてみる。 例 (1) 8 < 3xy = 3 xy = 1!23 弾性立体の構成方程式 3次元弾性立体の運動方程式を求めるためには、応力テンソル を求める方程式である構成方程式を導けばよい。 そうすれば、コーシーの運動方程式()に、その を代入することにより、運動方程式が確定する。微小体積要素の変位は、回転とひずみに分けられる例3 次の連立1次方程式を考える。 3x1 − 2x2 x3 4x4 = 7 x1 − 3x3 x4 = 5 2x1 − x2 9x3 = 0 この連立1次方程式は、次の行列の方程式でも表される。



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト


第4回講義 基礎数学
小学生とちがい、中学生以後はすべての文章題を方程式を使って解きます。 そして、高校入試数学の文章題の多くは、連立方程式で解く問題です。 この稿では、連立方程式を使って解く文章題の式のつくり方の基本をやさしく解説します。 ★文章題で連立方程式をつくるときの3つのポイント



文字が4つの連立方程式 Youtube



中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット



連立方程式 中学数学に関する質問 勉強質問サイト



問287 連立方程式と3つの自然数 オリジナルの高校数学の問題を掲載していきます



連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ



3 つの 連立 方程式
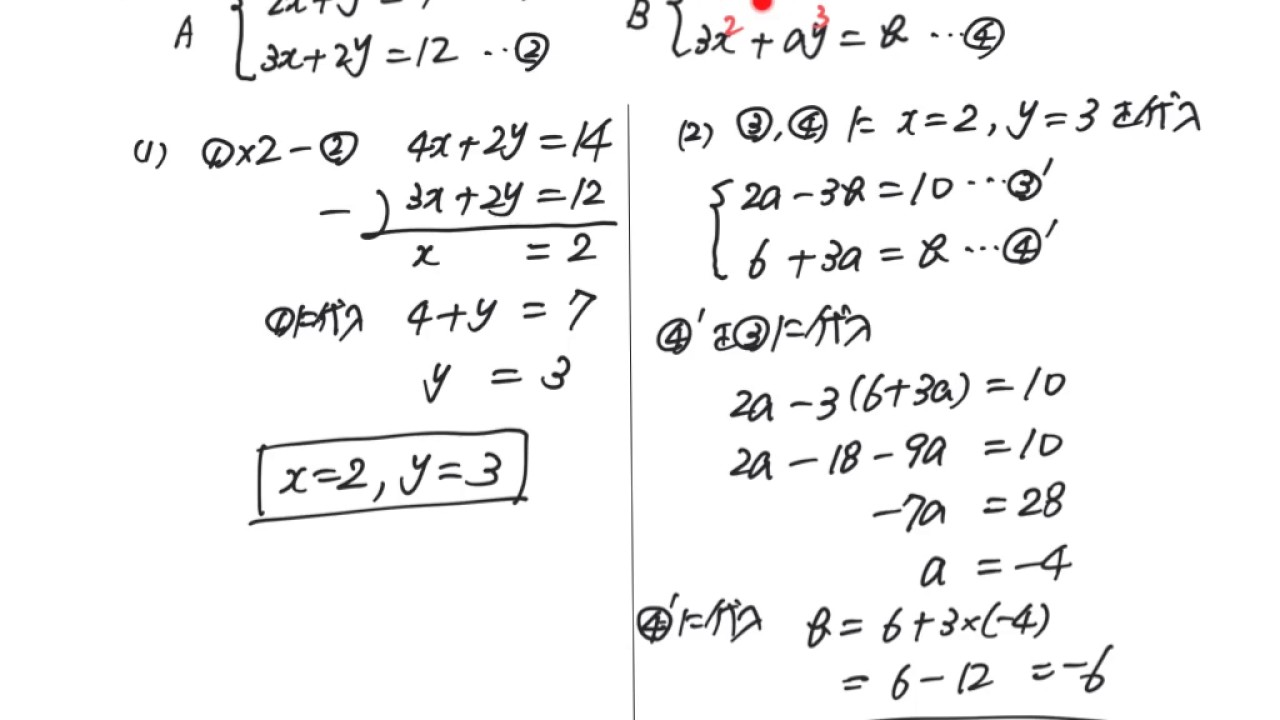


中2数学連立方程式 4つの式が同じ解を持つ Youtube


中学数学連立方程式至急お願いします ある選手が バスケットボール Yahoo 知恵袋



高校数学 2式が互いに対称な連立方程式 和と差で組み直せ 受験の月



連立方程式の解 xとyに代入して 式が成り立てばok 中学や高校の数学の計算問題


最高の3 つの 連立 方程式 の 解き方 ただぬりえ


至急 画像にある3つの連立一次方程式を拡大係数行列の簡約化でとく方法を教えて Yahoo 知恵袋



Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく


この連立方程式の解く順番を教えてください 3つの連立方程式の所が苦手でさっぱり Yahoo 知恵袋



高校数学 連立三角方程式 三角関数の相互関係 合成 加法定理の利用 受験の月



4元連立方程式の解き方を教えてください 1 x y z W 2 2 x 数学 教えて Goo



連立不等式 3つの不等式の解き方を問題解説 数スタ
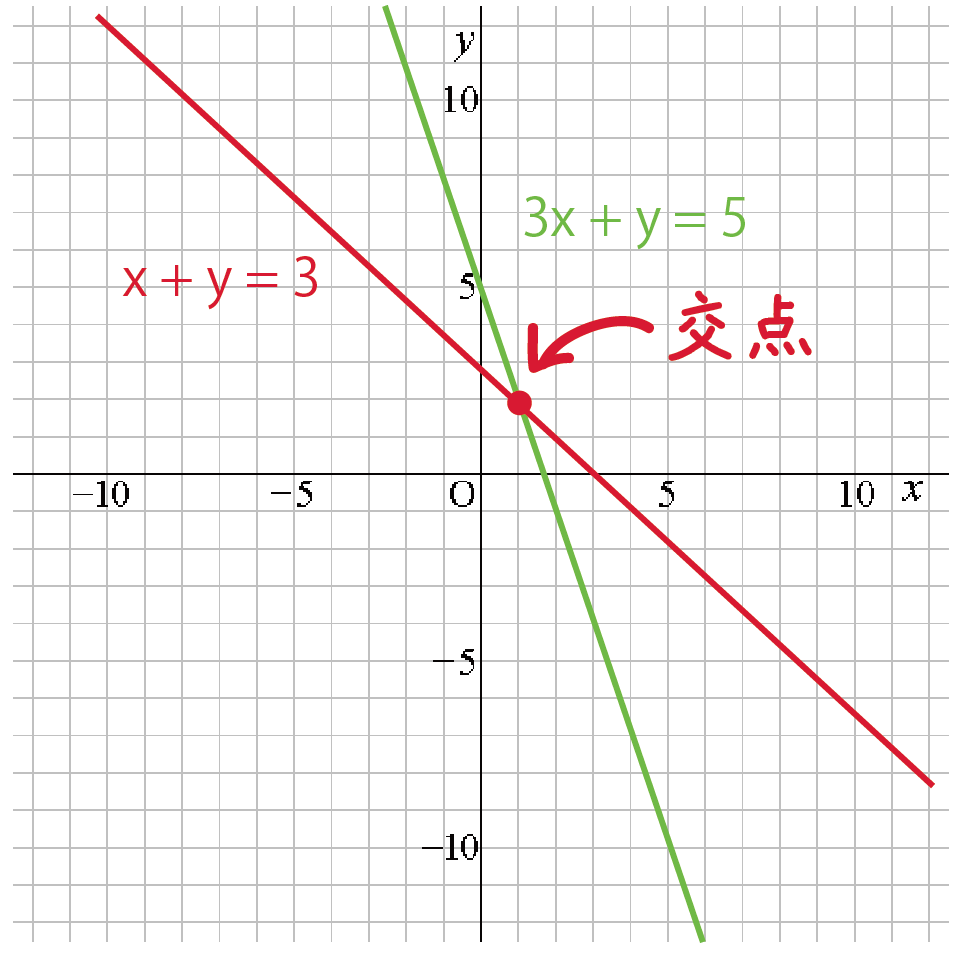


一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく


この問題は3つの式をそれぞれ60倍して連立方程式を解くでもあっていますか Yahoo 知恵袋



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく



未定係数を含む3元連立方程式の解 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信



3 つの 連立 方程式



高校数学 2元2次連立方程式3パターン 受験の月



連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ



連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学



7の問題で3つの式の連立方程式を解いてl M Nを求めよ 高校数学に関する質問 勉強質問サイト
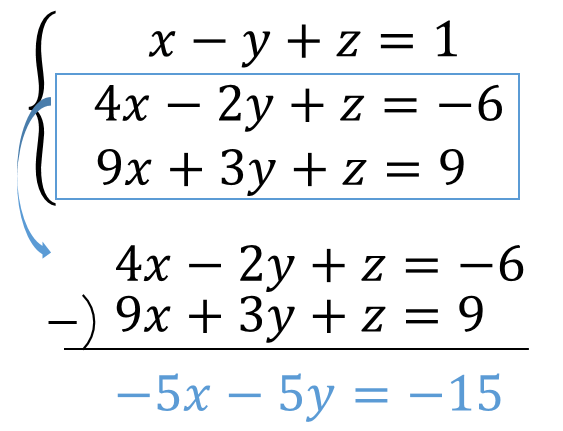


連立方程式 3つの文字 式の問題を計算する方法は 数スタ



三元連立方程式 2 中2数学 Youtube



物理 キルヒホッフの法則 は 電気回路 を解くカギ 理系大学院生が5分で解説 ページ 4 4 Study Z ドラゴン桜と学ぶwebマガジン


連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス
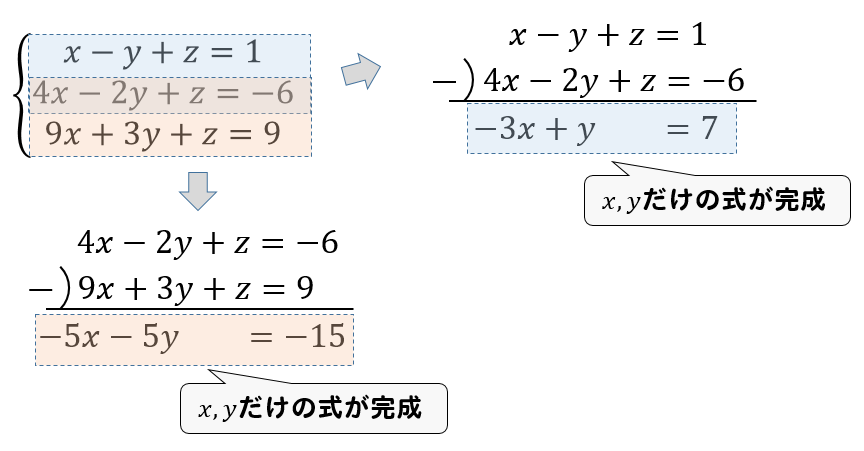


連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト



連立1次方程式の掃き出し法と行列の基本変形



3 つの 連立 方程式



中学2年生 数学 いろいろな連立方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



子供向けぬりえ ロイヤリティフリー3 元 2 次 連立 方程式 解き方



中2数学 a b cの連立方程式 練習編 映像授業のtry It トライイット



3 つの 連立 方程式



連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト



高校数学 3元連立1次方程式 一般型と循環型 受験の月



高校数学 3点を通る円の方程式の決定 練習編 映像授業のtry It トライイット



3つの連立方程式 コツ 2分で解説 3つの連立方程式のポイント Youtube



質問 数学 中学 の計算や 連立方程式の解き方について オンライン無料塾 ターンナップ



目指せノーミス 連立方程式3つの落とし穴 Youtube



3 つの 連立 方程式



Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



数学 内容解説資料v2



徹底解説 連立方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



連立方程式の2つの解き方 代入法 加減法 数学fun



3 つの 連立 方程式



3つの連立方程式の問題 解き方はこのようにすればバッチリだ 中学や高校の数学の計算問題



連立方程式 3つの文字 式の問題を計算する方法は 数スタ


3 つの 連立 方程式



Spi 文字が3つの連立方程式が10秒で解ける 勉強 Youtube スタディチューブ



7の問題で3つの式の連立方程式を解いてl M Nを求めよ 高校数学に関する質問 勉強質問サイト



文字が3つの時の連立方程式の解き方を教えて下さい Clear



2次関数26 連立3元1次方程式 怜悧玲瓏 高校数学を天空から俯瞰する



連立3元1次方程式 身勝手な主張


物理で3つの連立方程式が出てきたのですが 何回計算してもi1 Yahoo 知恵袋



3分でわかる 連立方程式の代入法と加減法をわかりやすく 合格サプリ
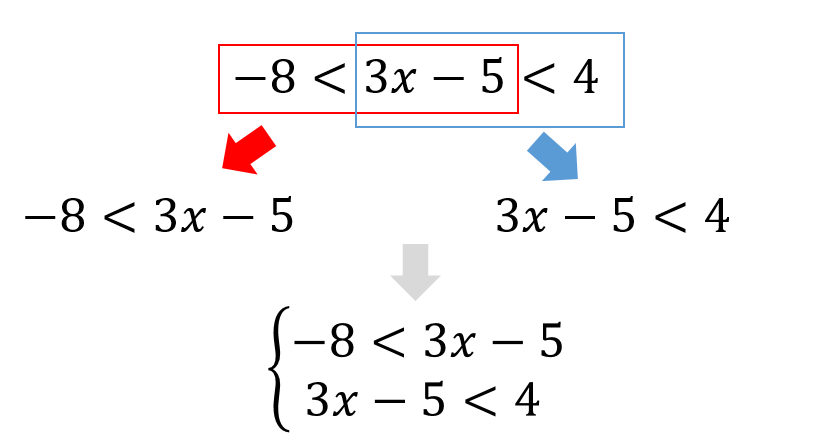


連立不等式 3つの不等式の解き方を問題解説 数スタ


最高の3 つの 連立 方程式 の 解き方 ただぬりえ
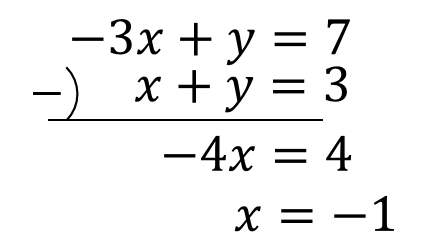


連立方程式 3つの文字 式の問題を計算する方法は 数スタ



連立方程式 3つの文字 式の問題を計算する方法は 数スタ



3 つの 連立 方程式



Math 超簡単 連立方程式の利用 働きアリ



3 つの 連立 方程式



1 と 3 の解き方と答えがわかりません 教えてほしいです Clear


第1章 連立方程式


第4回講義 基礎数学


連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点
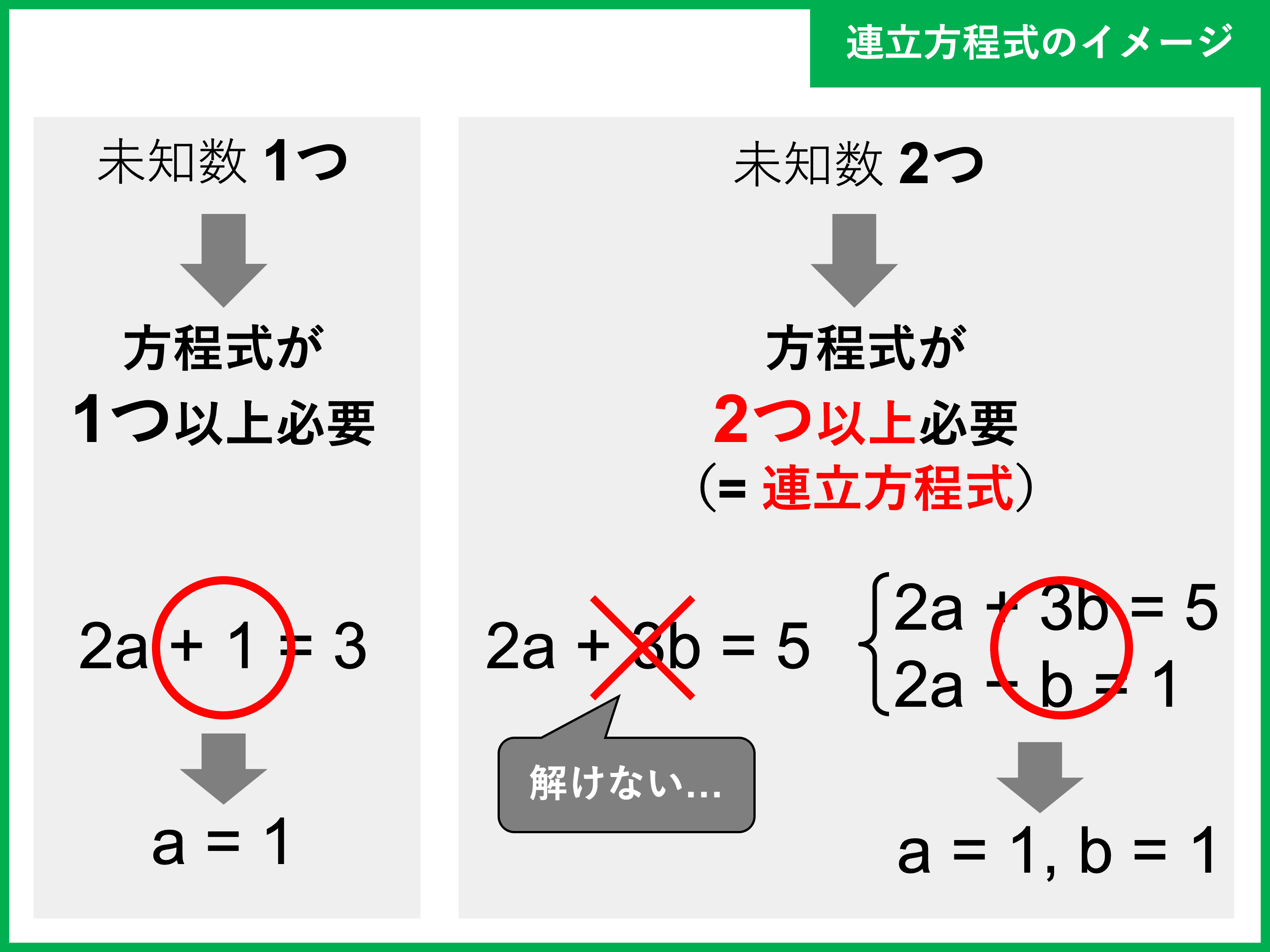


連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典
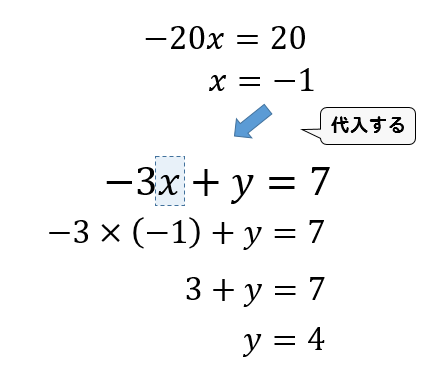


連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト


連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス
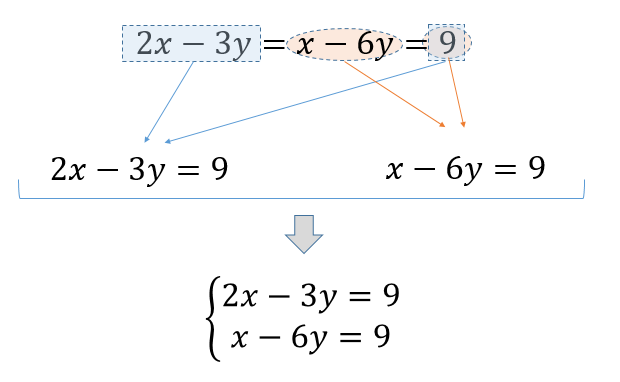


連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト



連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典


至急お願いします 空間ベクトルの連立方程式の解き方を教えてくださ Yahoo 知恵袋



数学中2 連立方程式とその解き方 中学数学に関する質問 勉強質問サイト



三つの連立方程式の解き方が良くわかりません Clear



連立方程式 Simultaneous Equations Youtube


Studydoctor三元連立方程式 2 中2数学 Studydoctor



連立方程式を解く時の流れを行列に当てはめてみよう 線形代数を宇宙一わかりやすく解説してみるサイト



徹底解説 連立方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ
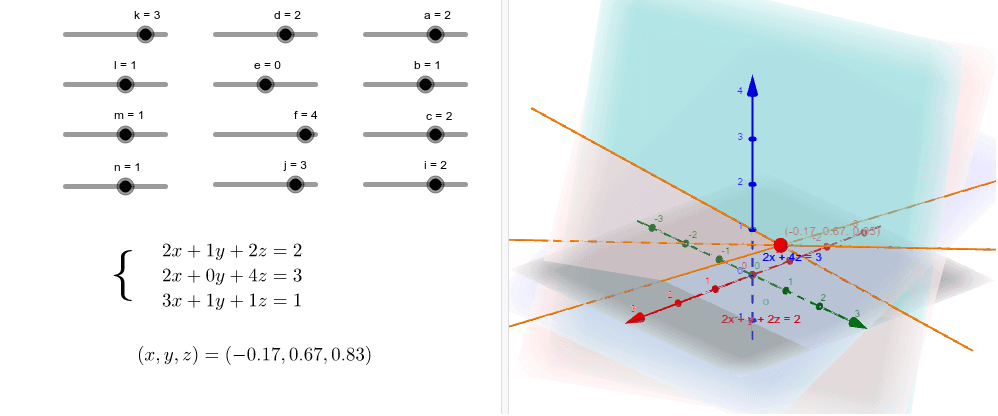


三元一次連立方程式 Geogebra


連立方程式の行列解



連立方程式 条件を 考えて 複数の答えを 絞り出す 名寄 算数数学教室より
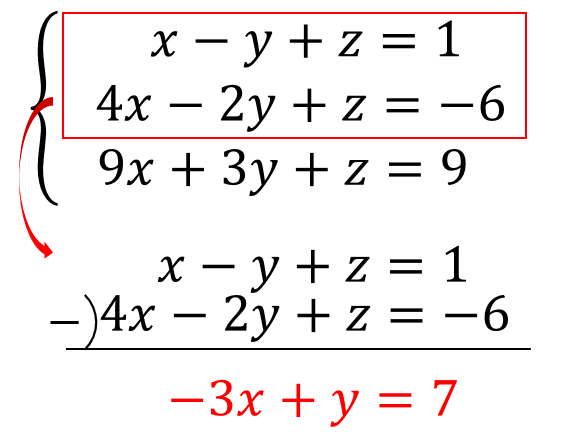


連立方程式 3つの文字 式の問題を計算する方法は 数スタ


連立方程式の行列解



0 件のコメント:
コメントを投稿